可視化モジュール `psiclone.visualization`

ここでは，可視化用のモジュール psiclone.visualiztion の関数群の使い方を見ていきます．このモジュールの主な関数は以下のとおりです：

draw_COT_labels() …… COT ラベルのみをレーブグラフの各辺近傍に描画
draw_barcode() …… パーシステントホモロジーとレーブグラフのバーコード図を描画
draw_bitmap() …… GrayscaleImage 型と整合する入力データ空間を描画
draw_contour() …… 等高線図を描画
draw_geometry() …… Geometry 型の入力データ空間を描画
draw_graph() …… レーブグラフのみを描画 (NetworkX)
draw_graph_markers() …… レーブグラフのノードとエッジを入力データ空間の座標で描画
draw_partition() …… レーブグラフに対応するパーティション図を描画
get_COT_constructions() …… COT 表現の再帰的構成と対応するパーティション情報を取得
get_barcode_data() …… バーコード図の情報を取得 (draw_barcode() に対応)
get_graph_markers_data() …… レーブグラフの座標情報を取得 (draw_graph_markers_data() に対応)
get_partition_data() …… パーティション図の構成情報を取得 (draw_partition() に対応)

可視化用の関数 draw_***() の多くは，あくまで初期的実験やチュートリアル導入を簡易的に行えるように用意されたものです．高度・専門的・発展的な可視化の目的では，これらの簡易関数を用いることは非推奨です．高度な可視化を行いたい場合は，Matplotlib などのライブラリの可視化関数を直接利用することを推奨しています．例えば，visualization モジュールは常に現在の Axes (matplotlib.pyplot.gca() = get current axes) に対して描画を行います．特定の Axes に描画したいなどより細かなカスタマイズを加えたい場合には，ユーザーが個別に可視化コードを組む必要があります．この場合，描画データ取得用の関数 get_***() を活用してください．

入力データの用意

import matplotlib.pyplot as plt
import numpy

import psiclone.visualization as vis
from psiclone.psi2tree import Psi2tree

まずは入力データ空間を用意します．チュートリアルと同じ方法で例を構成します．

from psiclone.util.convert import convert_array_to_geometry

x0, x1, y0, y1 = -3.0, 3.0, -2.5, 2.5
x, y = numpy.mgrid[x0:x1:15j, y0:y1:15j]
z = x + y * 1j
flow_domain = numpy.abs(z) >= 1.0
obstacle_domain = ~flow_domain

z = numpy.ma.masked_array(z, obstacle_domain)
W = z + 1.0 / z
data = numpy.imag(W)

table = numpy.ma.masked_array([x, y, data]).reshape((3, -1)).T
geom = convert_array_to_geometry(table, obstacles=[(0, 0)], int_grid=False)
geom

<psiclone.data.geometry.Geometry at 0x7f6d83eb6c00>

予め COT 表現も計算しておきます．

from psiclone.cot import to_str

psi2tree = Psi2tree(geom, threshold=1.0e-2)
psi2tree.compute()
psi2tree.get_tree().convert(to_str)

'a0(a2(L+,L-))'

基本的な描画関数

`psiclone.visualization.draw_bitmap()`

draw_bitmap() 関数は，GrayscaleImage 型と整合的な整数座標を持つ入力データ空間の高さ level を描画します．

vis.draw_bitmap(geom)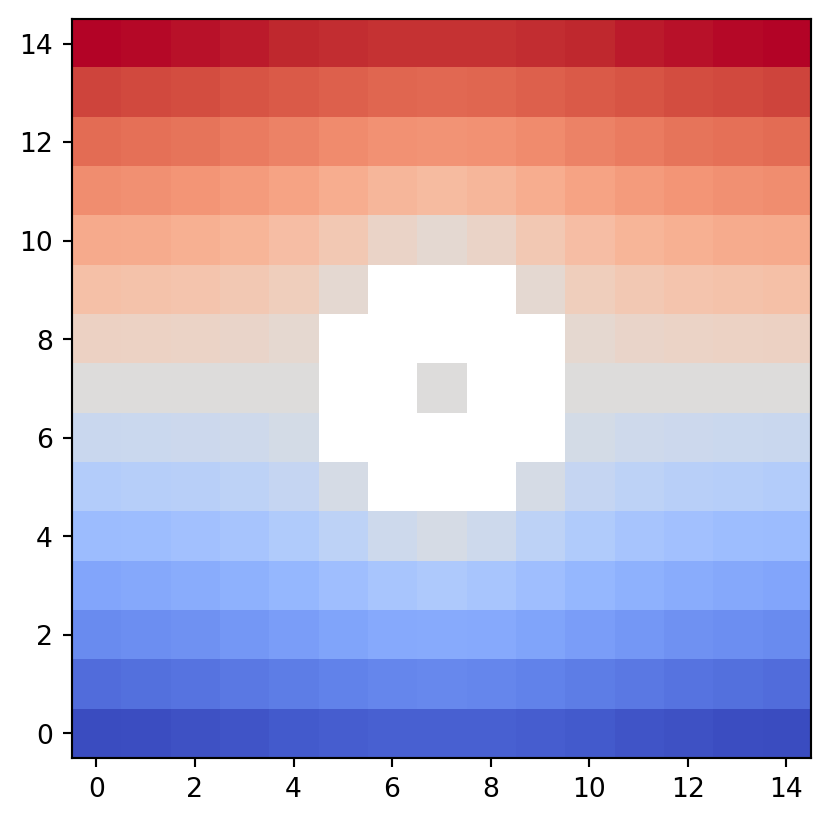

psiclone では，基本的に描画座標の原点を左下にとるように統一されています．これは，psiclone が流線図を解析するためのライブラリであるからです．matplotlib.pyplot.contour のデフォルト座標および数学的な慣習に合わせています．

`psiclone.visualization.draw_geometry()`

draw_geometry() 関数は，一般の Geometry 型の入力データ空間を描画します．bitmap=True を指定するとdraw_bitmap() を用います．bitmap=False のときは draw_networkx() を用います．以降の複数の描画関数でも同様の bitmap オプションが存在しています．

vis.draw_geometry(geom, bitmap=True)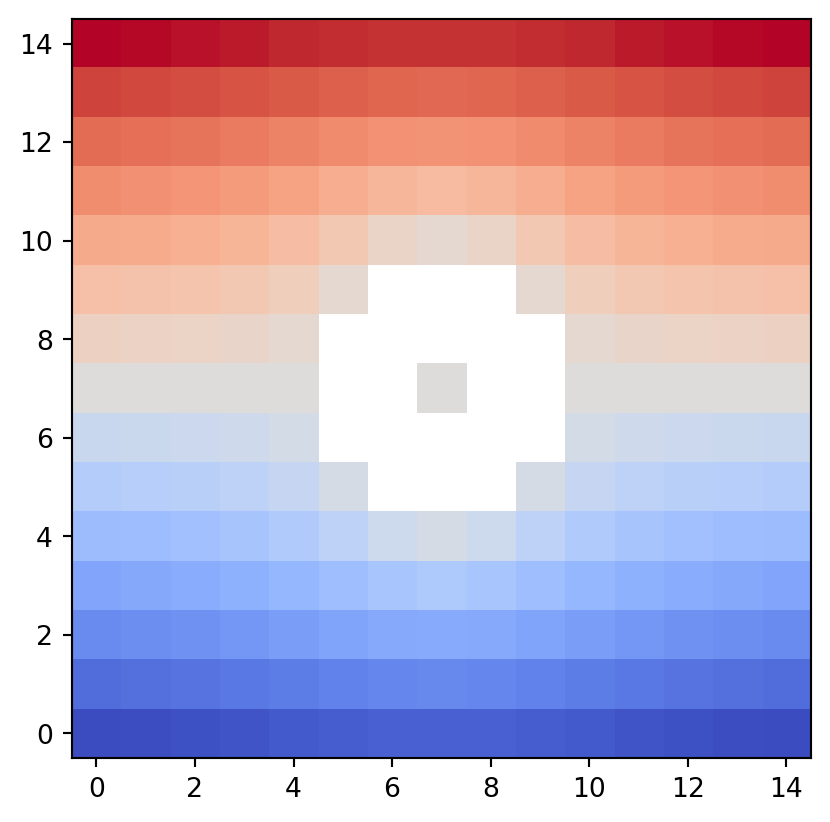

原則として，大きなデータの bitmap=False (NetworkX) による可視化は非推奨です．今の入力データ空間例は十分粗いので，figsize と dpi を大きく指定することで敢えて bitmap=False を指定してみます．

plt.figure(figsize=(7, 5), dpi=150)
vis.draw_geometry(geom, bitmap=False)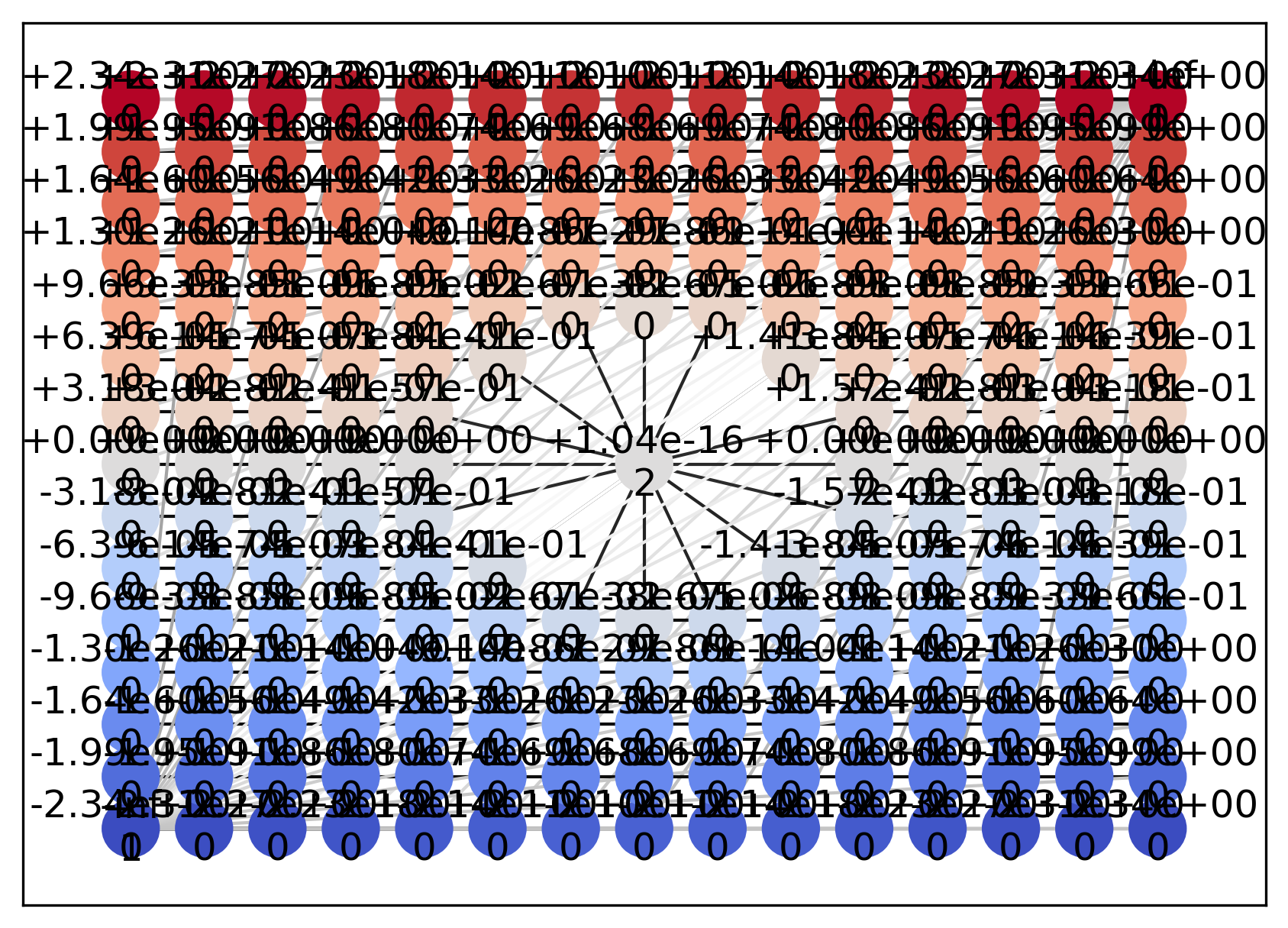

Psi2tree は計算の際にトポロジカルな境界条件を調整するため，入力データ空間の隣接構造を直接書き換えます．このため，内側境界だけでなく外側境界の周りにも複数のエッジが張られていることが確認できます．このようなトポロジー構造を直接確認したい場合以外，bitmap=False は指定しないでください．

`psiclone.visualization.draw_contour()`

draw_contour() 関数は入力データ空間の等高線図を描画します．より詳細に描画内容をカスタマイズしたい場合は，matplotlib.pyplot.contour() などを用いてください．

vis.draw_contour(psi2tree, bitmap=True)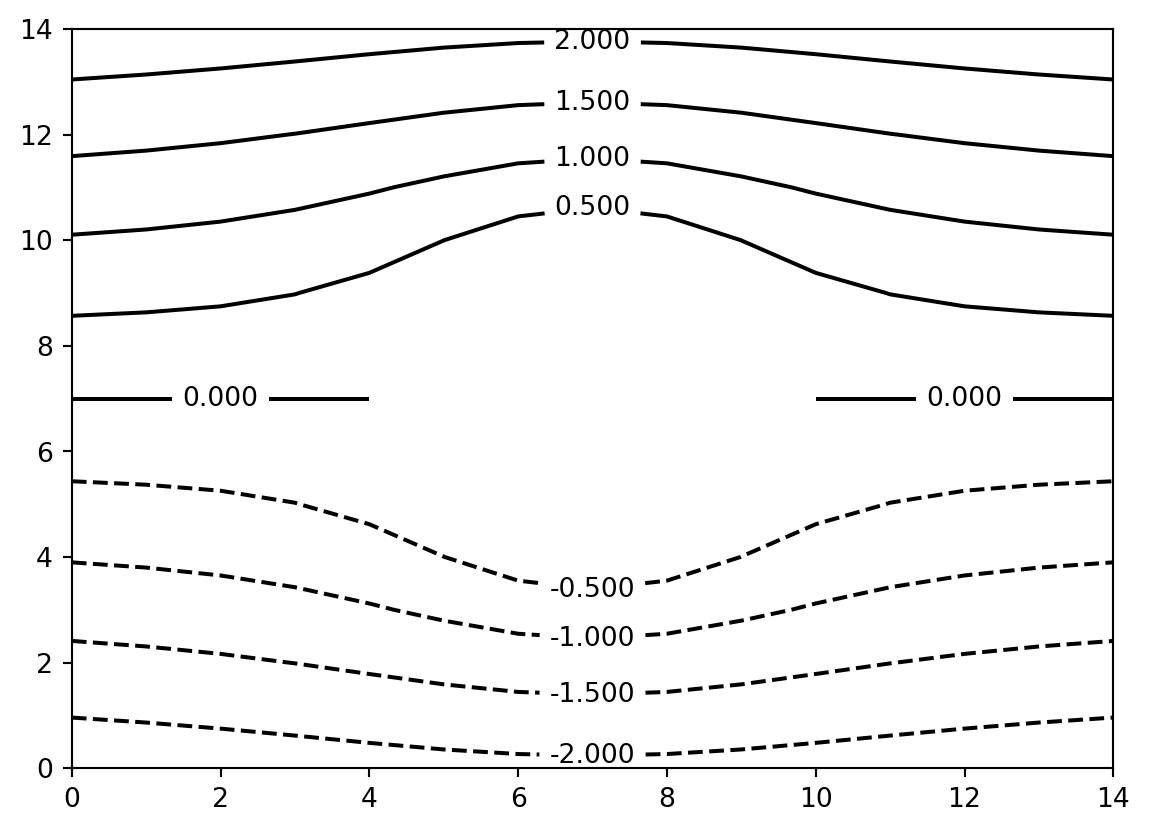

`psiclone.visualization.draw_partition()`

draw_partition() 関数は，Psi2tree の計算結果からパーティション図を描画します．これはレーブグラフによる同値類分割に対応します．

vis.draw_partition(psi2tree, bitmap=True)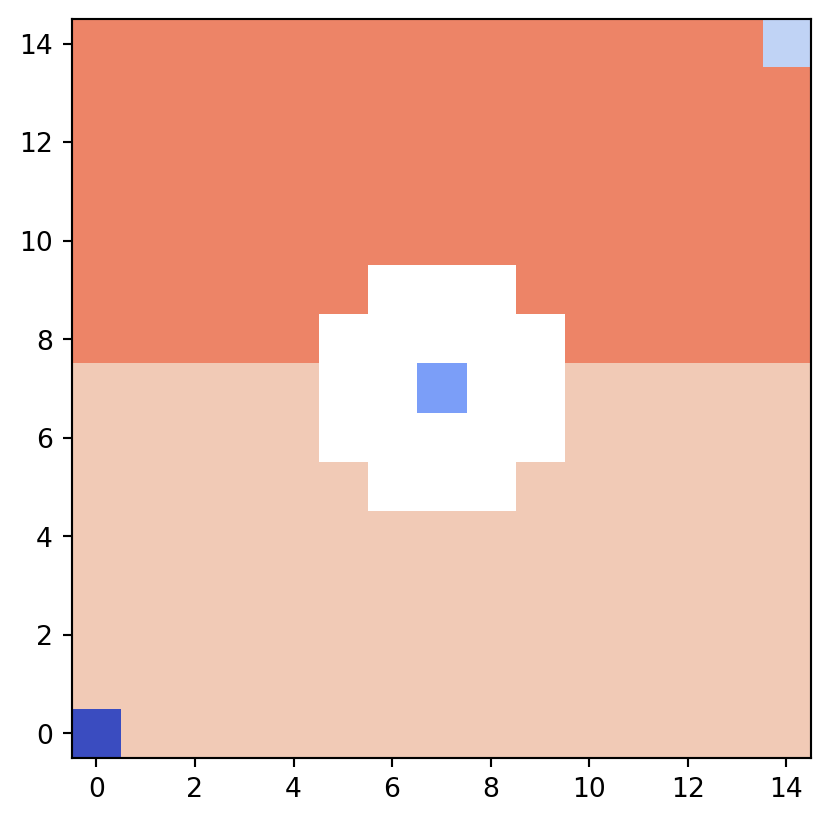

分割図では別々の同値類を識別しやすいよう色付けられています．数は少ないですがレーブグラフのノードに対応するピクセルも異なる色が割り当てられます．

`psiclone.visualization.draw_graph_markers()`

draw_graph_markers() 関数は入力データ空間の座標でレーブグラフを描画します．以下の例では，入力データ空間の座標に合わせるために，デフォルトの整数座標ではなく描画する座標範囲を指定していることに注意してください．

vis.draw_bitmap(
    geom,
    # 入力データ空間の座標と整合するよう extent を指定する
    extent=[x0, x1, y0, y1],
)
vis.draw_graph_markers(psi2tree, lw=3, edge_color="y-", node_color="g*")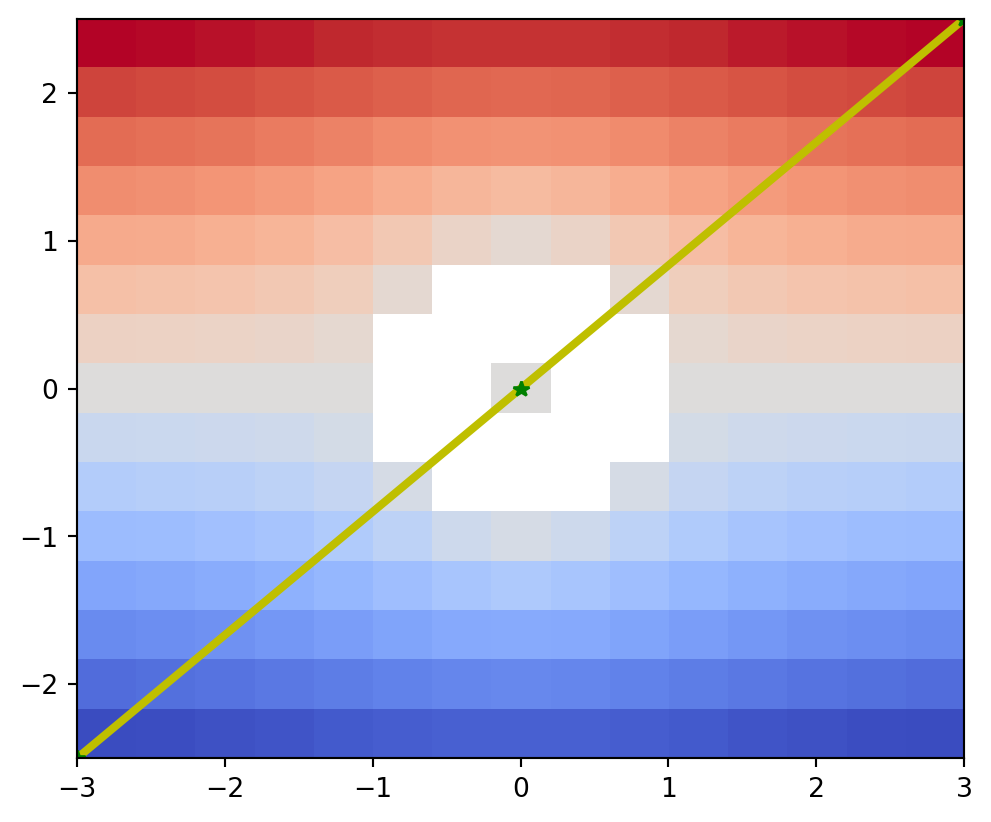

`psiclone.visualization.draw_COT_labels()`

draw_COT_labels() 関数は，レーブグラフの各エッジ周辺に，対応する COT ラベルを描画します．

vis.draw_partition(
    psi2tree,
    bitmap=True,
    # 入力データ空間の座標と整合するよう extent を指定する
    extent=[numpy.amin(x), numpy.amax(x), numpy.amin(y), numpy.amax(y)],
)
vis.draw_graph_markers(psi2tree, lw=1)
vis.draw_COT_labels(psi2tree)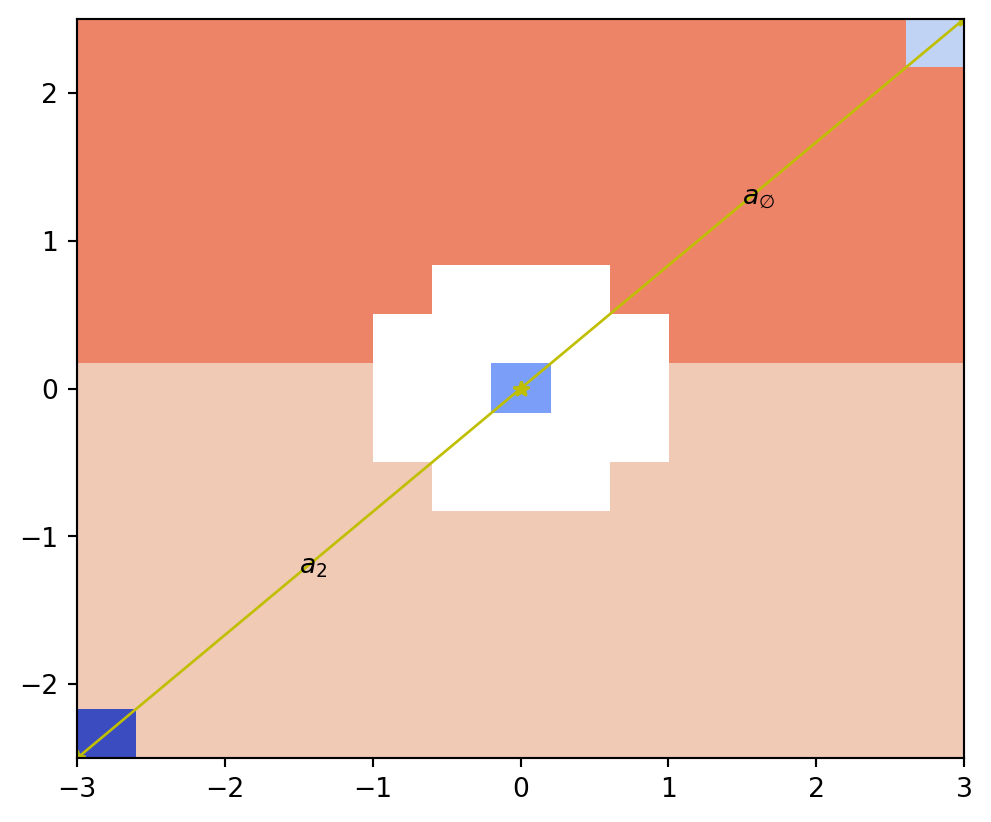

`psiclone.visualization.draw_barcode()`

draw_barcode() 関数は，入力データ空間から計算されたパーシステントホモロジーおよびレーブグラフのバーコード図を描画します．

vis.draw_barcode(psi2tree)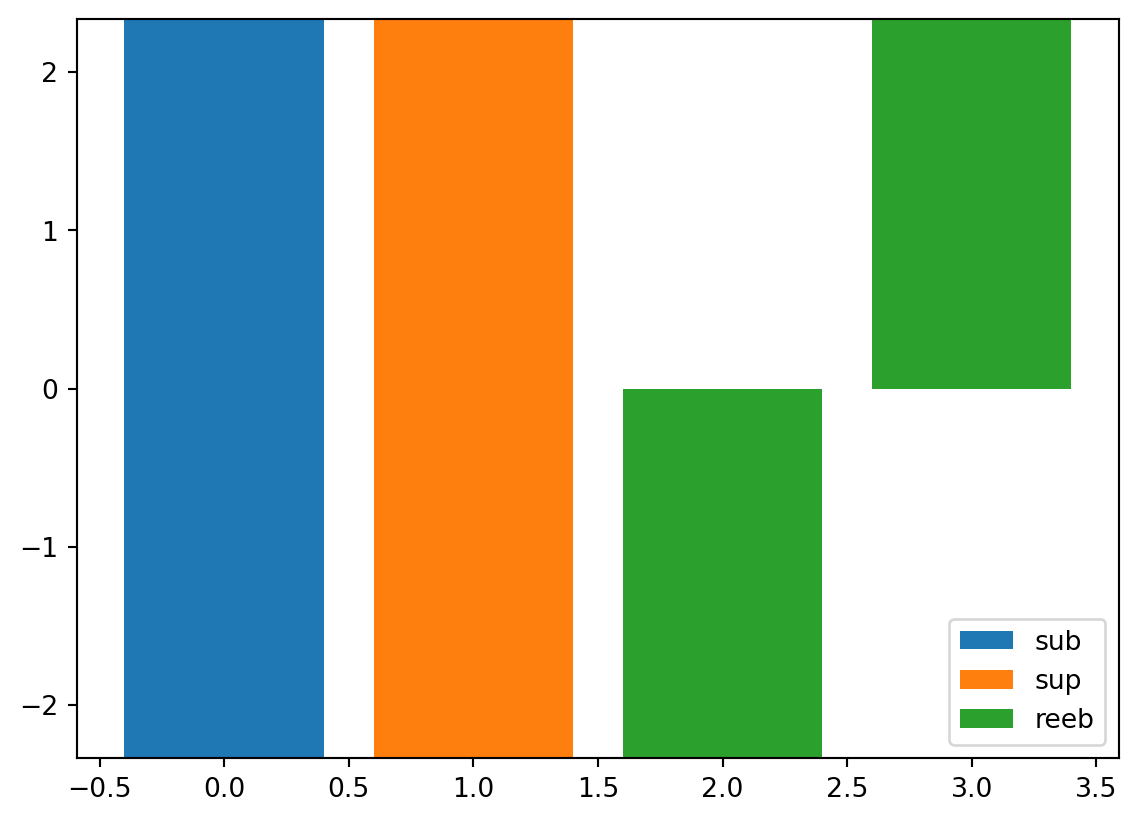

左から順に，

サブレベルフィルトレーションパーシステントホモロジーのバーコード図
スーパーレベルフィルトレーションパーシステントホモロジーのバーコード図
レーブグラフのバーコード図

になっています．バーコード図とは，高さ付きグラフの各エッジを対応する高さのバーで描画したものです．

発展的な描画の方法

より高度な可視化をするための関数の使い方を見ていきます．まずは，少し入力データを複雑なものに変更します．

x0, x1, y0, y1 = -3.0, 3.0, -2.5, 2.5
dx, dy = 129j, 129j  # 分割幅は実数，整数の虚数倍は分割数の指定
x, y = numpy.mgrid[x0:x1:dx, y0:y1:dy]
z = x + y * 1j
flow_domain = numpy.abs(z) >= 1.0
obstacle_domain = ~flow_domain

z = numpy.ma.masked_array(z, obstacle_domain)
W = z + 1.0 / z
perturbation = numpy.zeros_like(x)
perturbation += 0.2 * y
perturbation += 0.3 * numpy.ma.log(numpy.abs(z - (2.0 + 2.0j)))
perturbation -= 0.3 * numpy.ma.log(numpy.abs(z - (2.0 - 1.5j)))
data = numpy.imag(W) + flow_domain * perturbation

table = numpy.ma.masked_array([x, y, data]).reshape((3, -1)).T
geom = convert_array_to_geometry(table, obstacles=[(0, 0)], int_grid=False)
next(node for node in geom.nodes if node.geotype == 2).level = 0.0
psi2tree = Psi2tree(geom, threshold=0.1)
psi2tree.compute()

vis.draw_bitmap(geom)
plt.title(psi2tree.get_tree().convert(to_str))
plt.show()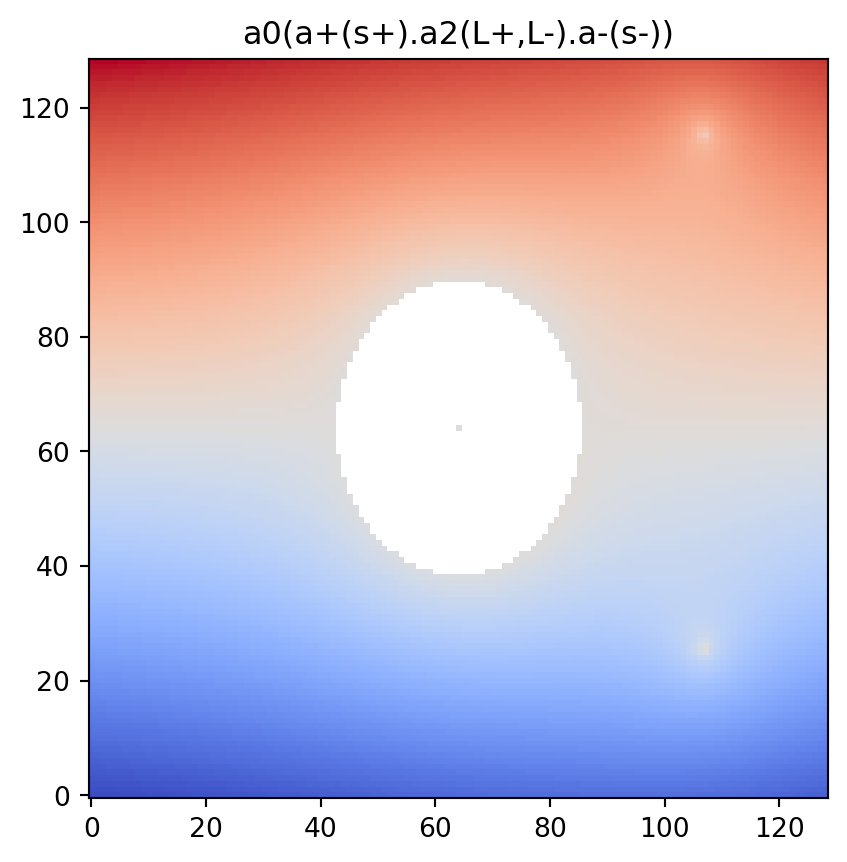

`psiclone.visualization.get_partition_data()`

get_partition_data() 関数はレーブグラフの同値類分割の情報を取得します．これは draw_partition() に対応したデータで，partition, vmin, vmax の三つ組です．partition は入力データ空間の高さ level 値に由来する分類値のリストになっています．

partition, vmin, vmax = vis.get_partition_data(psi2tree)

# flow_domain を転置 (ij-indexing) して描画
plt.imshow(flow_domain.T, origin="lower", cmap="gray")
vis.draw_bitmap(geom, node_color=partition, vmin=vmin, vmax=vmax)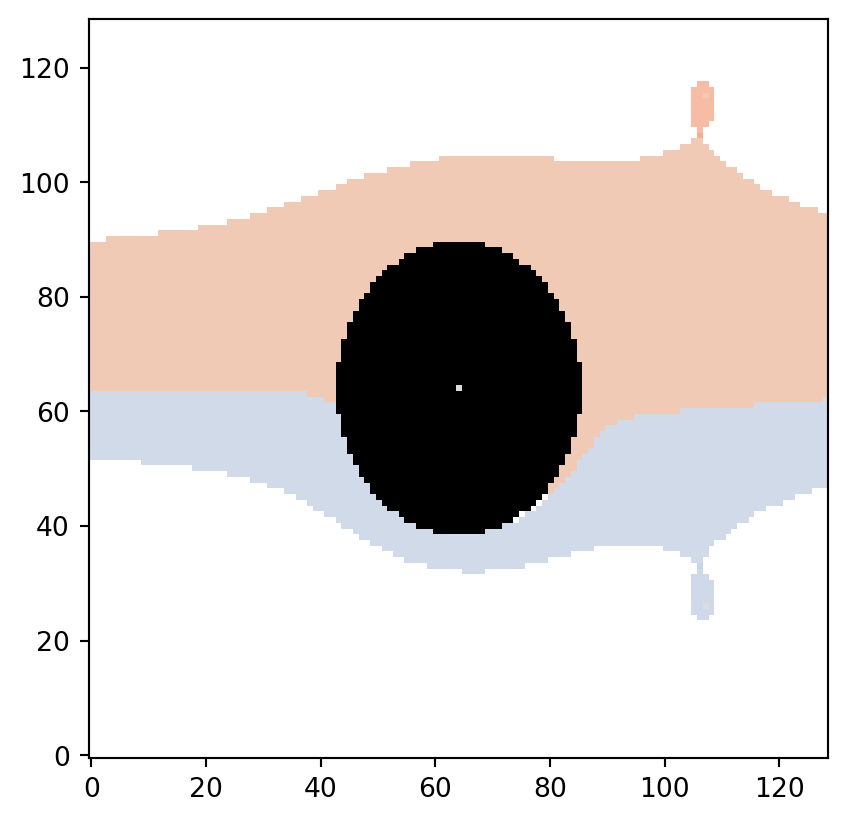

ここでは Psi2tree が一様流れの計算を行ったため，入力データ空間 geom に level 値 $\pm \infty$ の仮想点（無限遠点）が追加されています．そのため，一部の同値類は値が $\pm \infty$ になっています．トポロジカルには流れの下流に向かって最も左側が $+ \infty$ の同値類，最も右側が $- \infty$ の同値類に分類されます．

vmin と vmax は，partition ではなく元の入力データの有界な level 値の中での最小値および最大値です．外側境界までトポロジカルに近いところに最小値・最大値があると $\pm \infty$ のいずれかに分類されるため，実際には partition の中に vmin, vmax が含まれないことがあります．元のデータと整合するカラーレンジでパーティション図を描画したい場合は vmin と vmax を適切に利用するのが良いでしょう．

vmin, numpy.amin(data), vmax, numpy.amax(data)

(np.float64(-2.763353687123051),
 np.float64(-2.7529496539518234),
 np.float64(2.763353687123051),
 np.float64(2.763353687123051))

また，ノイズ除去の影響でパーティションには「どこにも分類されない部分」が含まれます．これは partition の中では None として表現されます．

# None の個数をカウント
len([i for i, x in enumerate(partition) if x is None])

discrete=True を指定すると，入力データの level 値の代わりに新たに割り振る整数値によって同値類の分割を表現します．この場合， $\pm \infty$ の値は含まれません．この場合，partition は optional int 値のリストになります．

plt.imshow(flow_domain.T, origin="lower", cmap="gray")
partition, vmin, vmax = vis.get_partition_data(psi2tree, discrete=True)
vis.draw_bitmap(geom, node_color=partition, vmin=vmin, vmax=vmax)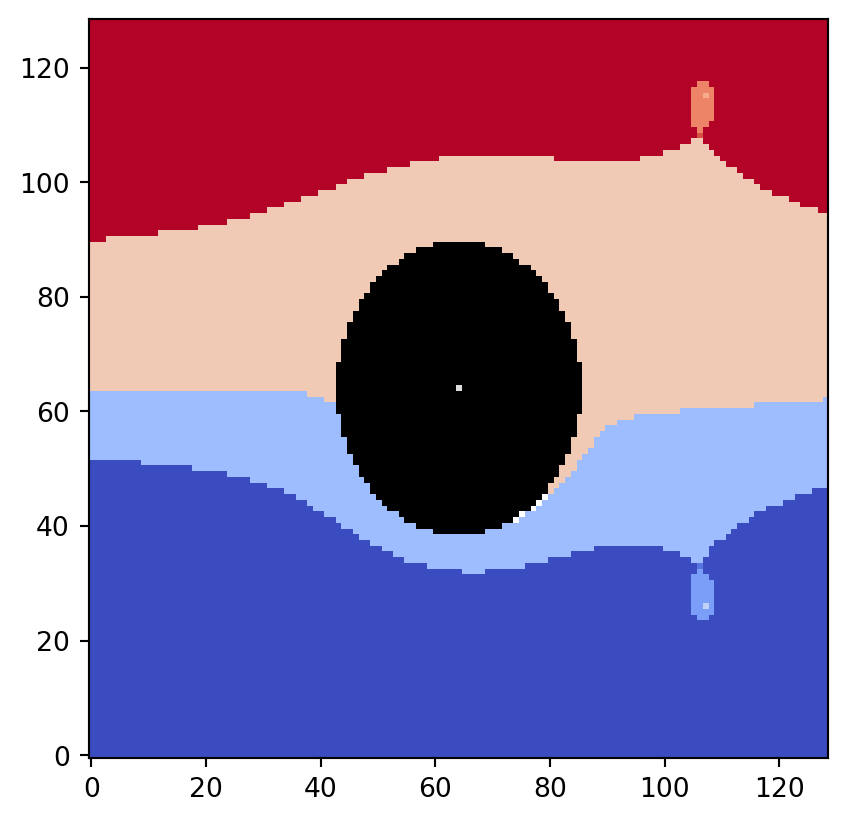

`psiclone.visualization.get_COT_constructions()`

get_COT_constructions() 関数は，COT 表現の再帰的構成と対応するレーブグラフ同値類の情報を取得します．COT ノードオブジェクトをキーとして，同値類の情報が格納された辞書式リストが得られます．

constructions = vis.get_COT_constructions(psi2tree)

for cot_node, partition in constructions.items():
    print(f"{cot_node.label()}: key={cot_node}\tvalue={numpy.array(partition)}")

a0: key=<psiclone.cot.TreeA0 object at 0x7f6d28dfaff0>  value=[3 3 3 ... 4 2 0]
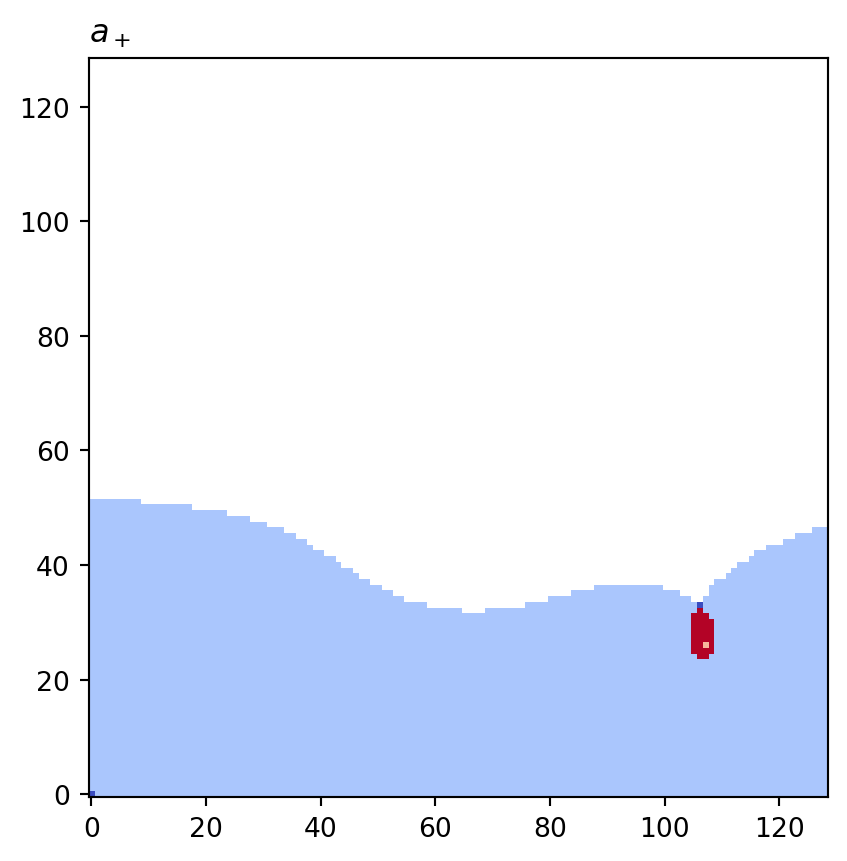
a+: key=<psiclone.cot.TreeA object at 0x7f6d28dfbf20>   value=[1 1 1 ... None 0 None]
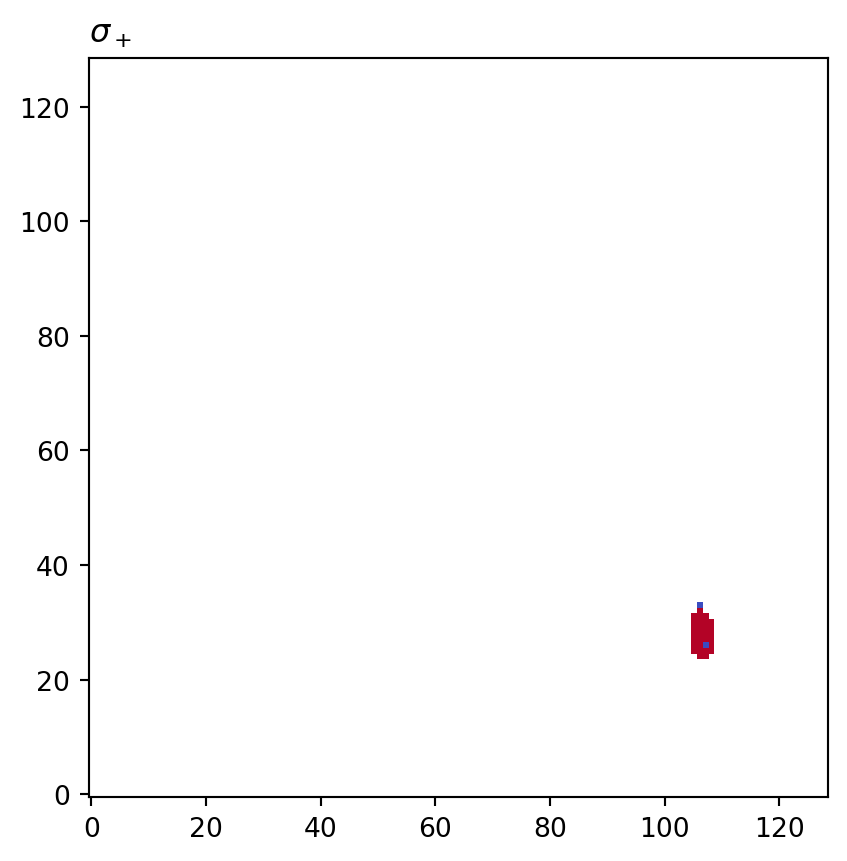
s+: key=<psiclone.cot.Genus object at 0x7f6d2b4a2ab0>   value=[None None None ... None None None]
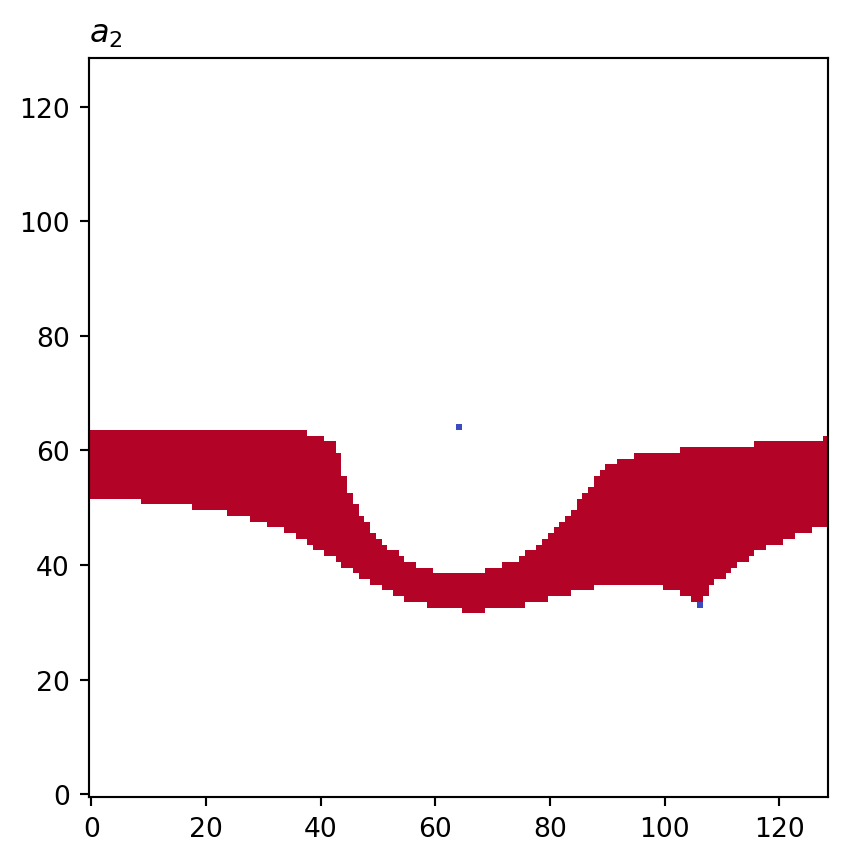
a2: key=<psiclone.cot.TreeA2 object at 0x7f6d290fe6c0>  value=[None None None ... 0 None None]
a-: key=<psiclone.cot.TreeA object at 0x7f6d290bfd40>   value=[None None None ... 0 None None]
s-: key=<psiclone.cot.Genus object at 0x7f6d28e75070>   value=[None None None ... None None None]

各同値類は，入力データ空間のノード配列と対応するサイズ・並びの optional float 値のリストです．

cot_node = next(iter(constructions.keys()))
len(constructions[cot_node]) == len(geom.nodes)

True

これらのリストは，draw_bitmap または draw_geometry の node_color オプションに渡すことができます．

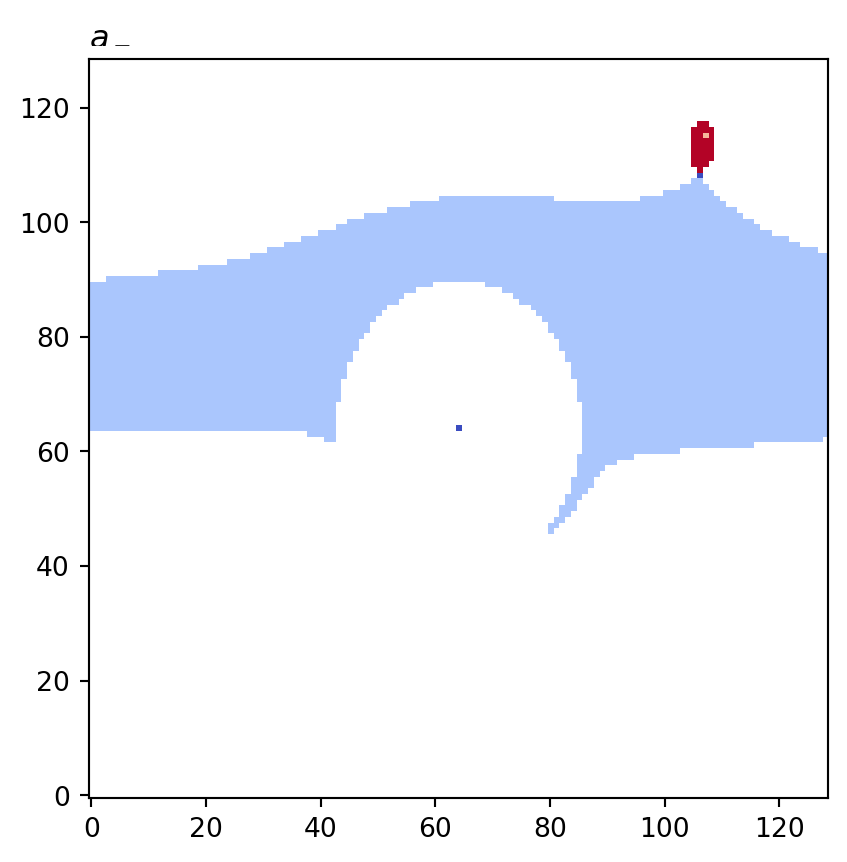
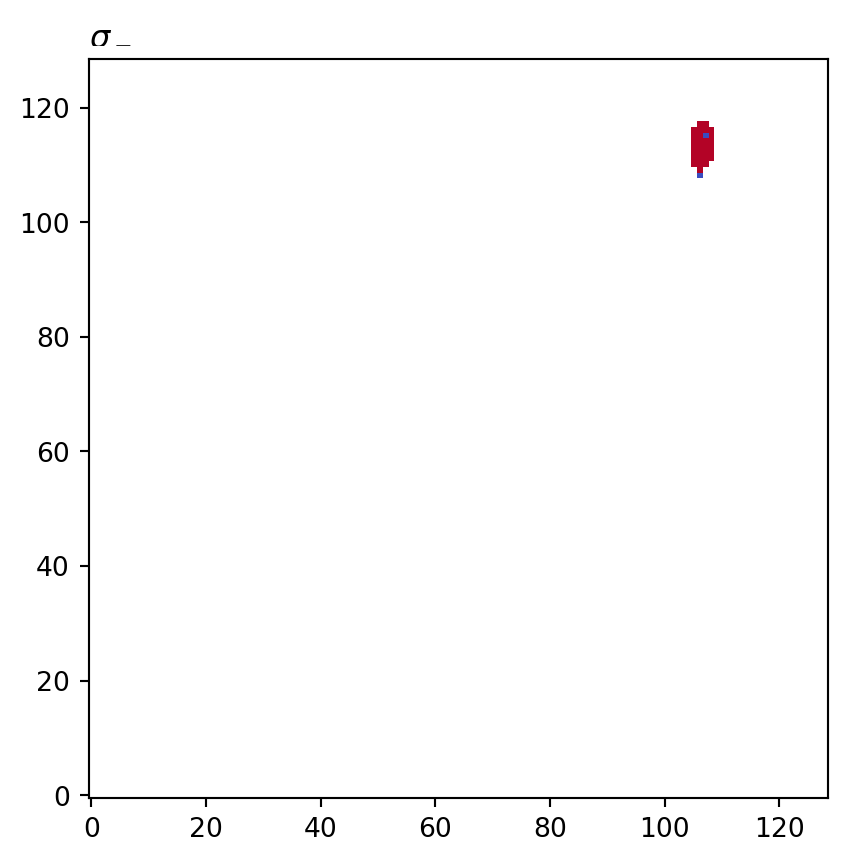
for cot_node, partition in constructions.items():
    tex = cot_node.label(tex=True)
    vis.draw_bitmap(geom, title=f"${tex}$", node_color=partition)
    plt.show()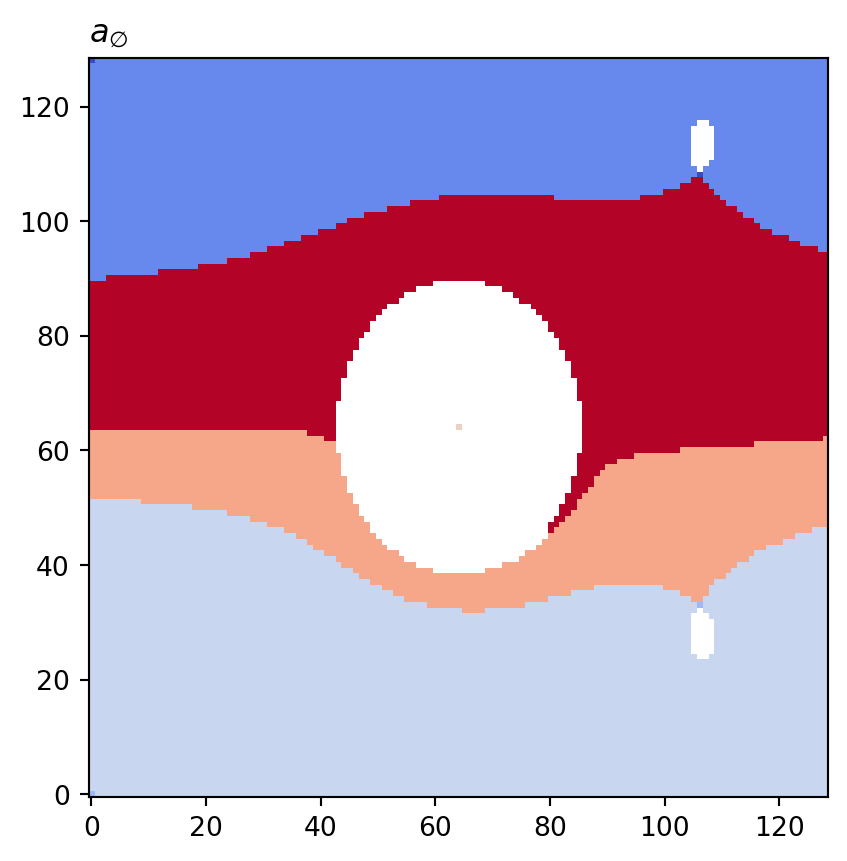

`psiclone.visualization.get_graph_markers_data()`

get_graph_markers_data() 関数は，レーブグラフを入力データ空間の座標で描画するための情報を取得します．これは draw_graph_markers() 関数に対応したデータで，lines, points の二つ組です．

lines, points = vis.get_graph_markers_data(psi2tree)

vis.draw_partition(psi2tree, bitmap=True, extent=[x0, x1, y0, y1])
for line in lines:
    plt.plot(line[0], line[1], "black", lw=1)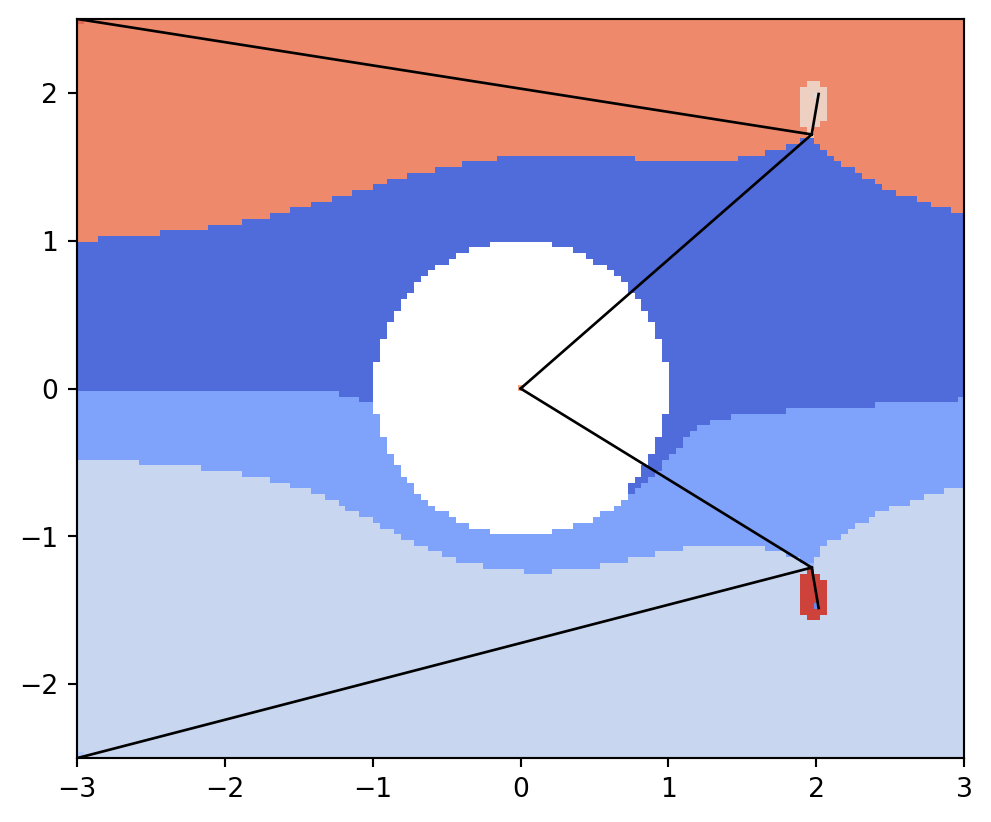

vis.draw_partition(psi2tree, bitmap=True, extent=[x0, x1, y0, y1])
plt.scatter(points[:, 0], points[:, 1], s=150, c="black", marker="*")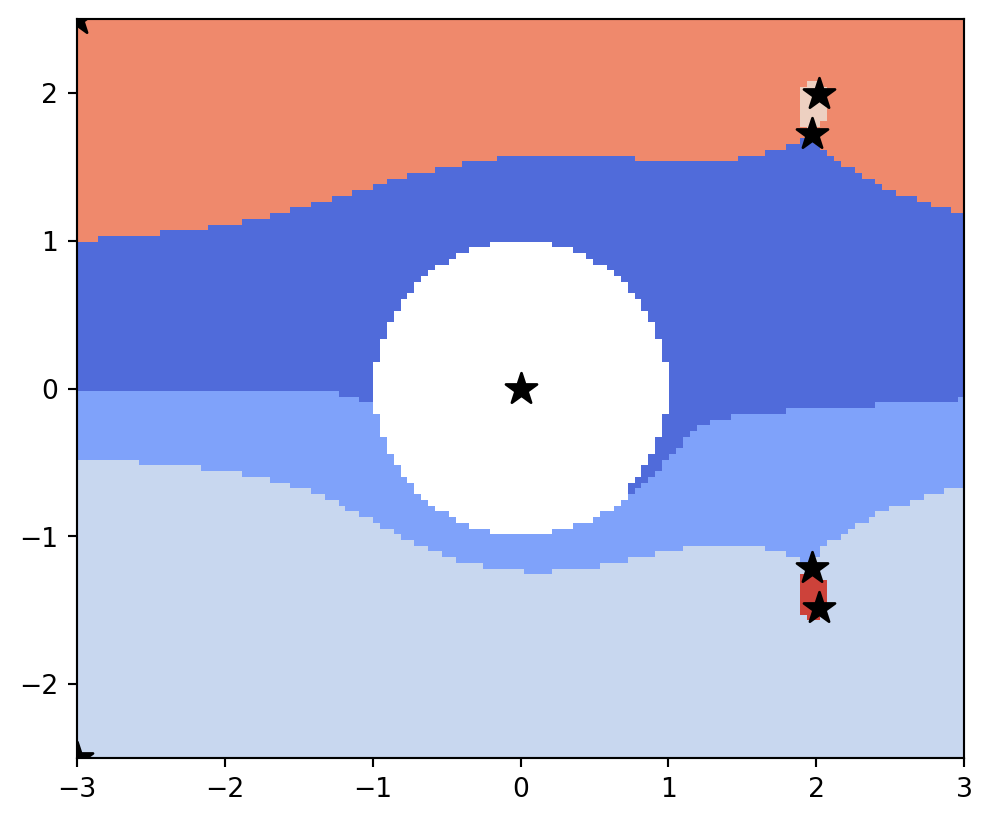

`psiclone.visualization.get_barcode_data()`

get_barcode_data() 関数はバーコードの情報を取得します．これは draw_barcode() に対応したデータで，文字列 ‘sub’, ‘sup’, ‘reeb’ をキーとする辞書式リストが得られます．これはそれぞれ，サブレベルパーシステントホモロジー，スーパーレベルパーシステントホモロジー，レーブグラフに対応するバーコードを表現します．各バーコードは，配列 x, y0, y1 の三つ組で構成されています．x はバーの系列番号，y0 はバーの下限値，y1 はバーの上限値です．

vis.get_barcode_data(psi2tree)

{'sub': (array([0, 1]),
  array([-2.75294965,  0.55322506]),
  array([2.76335369, 1.08143079])),
 'sup': (array([ 2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15]),
  array([-0.02617826,  0.00358474,  0.01381636,  0.02492754,  0.03030266,
          0.03121934,  0.05834316,  0.06569003,  0.06629733,  0.07192172,
          0.07369314,  0.07440814,  0.07892039,  2.76335369]),
  array([-0.50588341, -2.75294965, -2.75294965, -2.75294965, -2.75294965,
         -2.75294965,  0.02752536,  0.06562705,  0.02152453,  0.03687794,
          0.05984956,  0.04302202,  0.05388596, -2.75294965])),
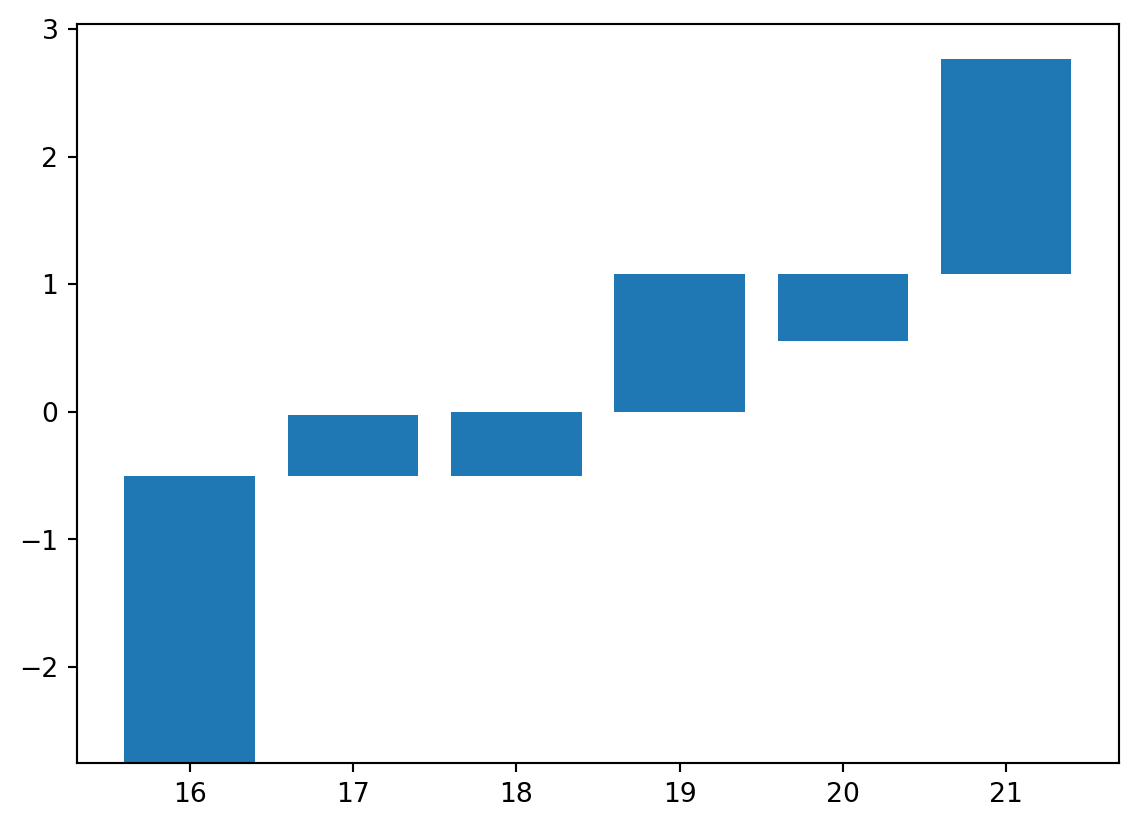
 'reeb': (array([16, 17, 18, 19, 20, 21]),
  array([-2.75294965, -0.50588341, -0.50588341,  0.        ,  0.55322506,
          1.08143079]),
  array([-0.50588341, -0.02617826,  0.        ,  1.08143079,  1.08143079,
          2.76335369]))}

x, y_bottom, y_top = vis.get_barcode_data(psi2tree)["reeb"]

plt.bar(x, y_top - y_bottom, bottom=y_bottom)