import matplotlib.pyplot as plt
import numpypsiclone.util モジュール
psiclone には,複雑な形状の入力空間データを取り扱うための psiclone.util モジュールが用意されています.その主な関数は以下のとおりです:
psiclone.util.convert.convert_array_to_geometry()…… 欠損のある表形式グリッドデータの多重連結領域への変換psiclone.util.mcdomain.mcdomain_to_geometry()…… 欠損のあるグリッドデータの多重連結領域への変換
いずれも,入力空間が多重連結領域である場合を想定した作りになっています.ただし,欠損がないシンプルな単連結長方形状の入力空間を取り扱うときは GrayscaleImage の利用を検討してください.
GrayscaleImage() |
convert_array_to_geometry() |
mcdomain_to_geometry() |
|
|---|---|---|---|
| 入力空間 | 単連結長方形領域 | 多重連結長方形領域 | 多重連結領域 |
| グリッド型 | 一様格子(座標が整数) | 非一様格子(非整数座標を許す) | 一様格子(座標が整数) |
| 適した流れ | 一様流れ/有界流れ | 一様流れ/有界流れ | 有界流れ |
| 変換元のデータ形式 | 二次元配列 (画像) | 二次元配列 | |
| 内部障害物(境界) | 未対応 | 障害物代表点をユーザが指定 | 障害物は自動判定 |
| 欠損・マスク対応 | 未対応 | 対応 | 対応 |
| ユーザが指定 | numpy.average で自動計算 |
オプションで計算方法を指定 |
いずれの方法にもそれぞれメリット・デメリットがあり,状況に応じて適切な選択が必要です. 特に,TFDA では境界の扱いが重要であり,その設定を間違えると思ったとおりの解析結果が出ません. util モジュールの関数群は,いずれも簡易的な解析のために用意された関数に過ぎず,個別の状況に応じた境界条件の検証が重要となります. また,さらに複雑な幾何形状を持つ入力データ空間を扱いたい場合は,メッシュ構造データの扱い方も参照してください.
psiclone.util.convert を用いて一様流れを解析する場合
psiclone.util.convert.convert_array_to_geometry() 関数を用いて,中心に障害物が一つ置かれている問題設定で (x, y, z) が複数並ぶ入力データを読み込み,一様流れの COT 表現に変換します.
import psiclone.visualization as vis
from psiclone.psi2tree import Psi2treeここでは,入力空間は非有界な円除外領域とします.ただし,非有界といっても,適当な長方形領域で打ち切って有界にしたものを考えます.
y, x = numpy.mgrid[-3:3:101j, -3:3:101j]
z = x + y * 1j
flow_domain = numpy.abs(z) >= 1.0
obstacle_domain = ~flow_domain
plt.imshow(flow_domain, cmap="gray", origin="lower")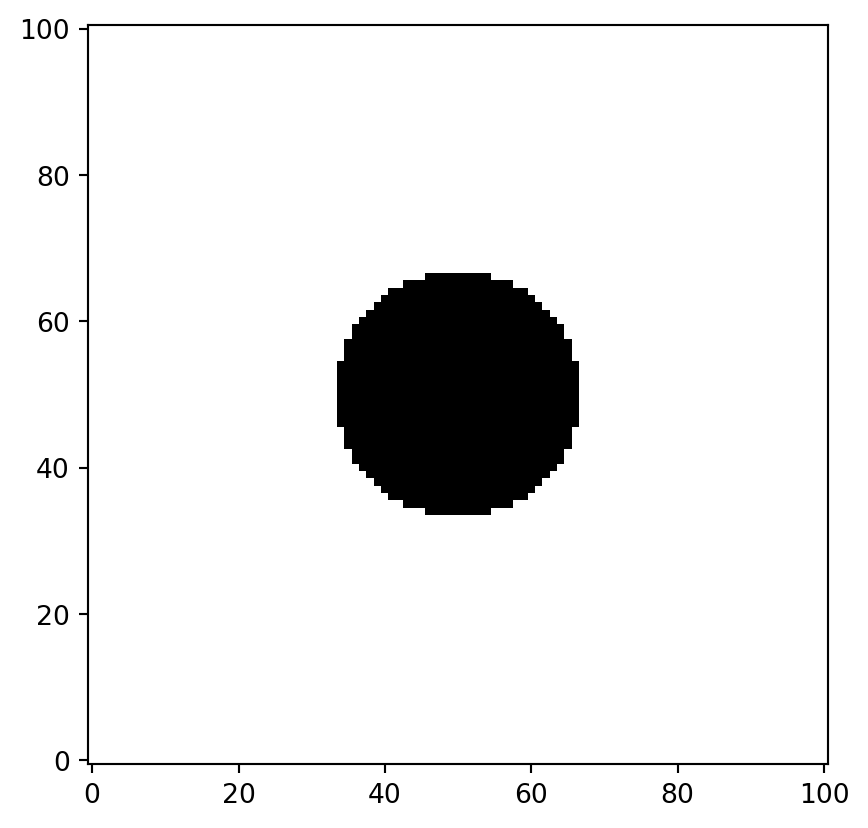
mesh grid を作成して,虚数単位 1j を用いて複素変数
その上のデータを表現するには,numpy.ma.masked_array を利用すると便利です.これは,データ欠損領域をマスクを用いて指定できる特殊な配列です.データ欠損領域がある以外は,通常の numpy.ndarray と同様に扱うことが可能です.さて,複素変数 masked_array を用いて,次のように流線関数を用意します.
z = numpy.ma.masked_array(z, obstacle_domain)
W = z + 1.0 / z
data = numpy.imag(W)
plt.imshow(data, cmap="coolwarm", origin="lower")
plt.contour(data, colors="k")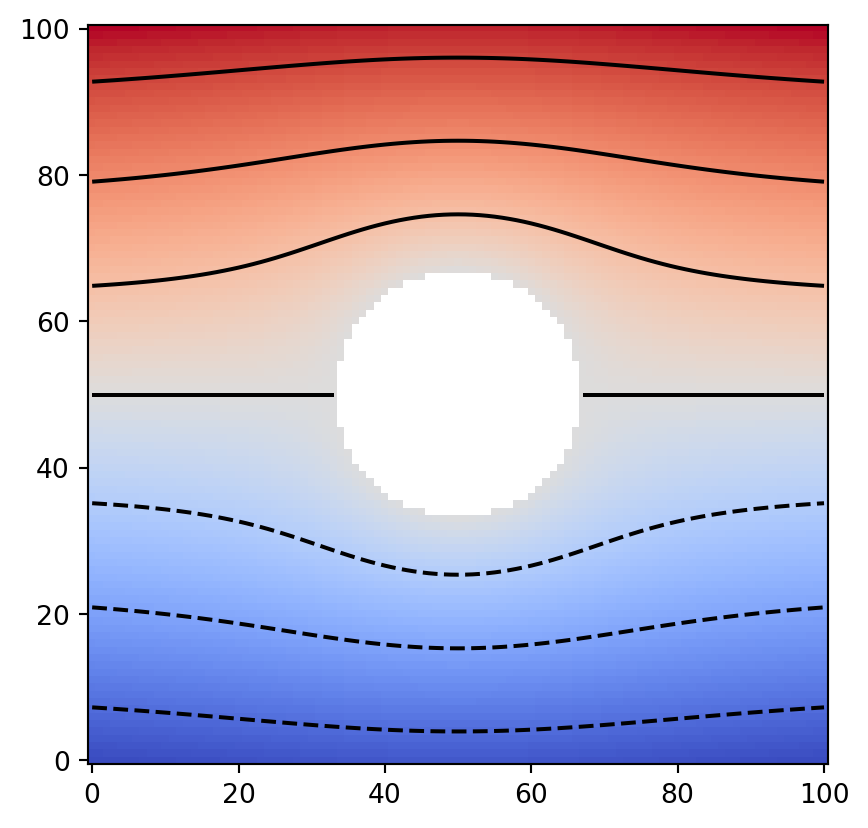
これで,円形障害物の周りを流れる一様流のテストデータが作れました.これを Geometry に変換していきます.
table = numpy.ma.masked_array([x, y, data]).reshape((3, -1)).T
table.shape(10201, 3)障害物のある一様流の設定で Geometry を構成するユーティリティ関数 psiclone.util.convert.convert_array_to_geometry() を用います.そのために,まず nan を用いてデータ欠損領域を表現したデータや,単純にデータ欠損領域のエントリーを含まない表データでも構いません.)
この関数には,色々なオプション引数がありますが,ここでは障害物を指定する引数 obstacles に一つの障害物の座標だけを指定します.各障害物ごとに代表点の座標を一つだけ指定すれば十分です.この例では原点を指定しています.
from psiclone.util.convert import convert_array_to_geometry
geom = convert_array_to_geometry(table, obstacles=[(0, 0)])
geom, len(geom.nodes), len(geom.edges)(<psiclone.data.geometry.Geometry at 0x7fb5d84967b0>, 9325, 18476)これで入力空間のデータが用意できました.構成した geom が上と同じデータになっているか,確認してみましょう.
vis.draw_geometry(geom, bitmap=True)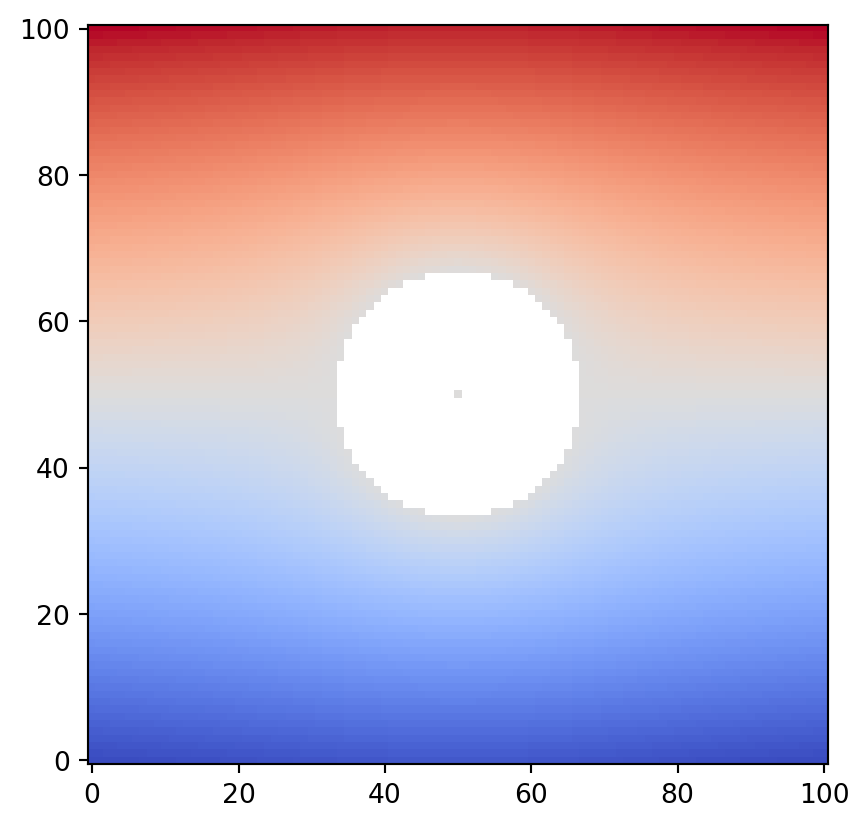
よく見ると,障害物の中央に指定した代表点が描かれていることに注意してください.このピクセルは,内部境界の境界データの平均値で描かれています.障害物ノードの属性値を確認してみましょう.障害物ノードは geotype として 2 (Geotype.OTHRES) 以上の値が設定されます.
from psiclone.data import Geotype
obstacle_node = next(node for node in geom.nodes if node.geotype >= Geotype.OTHERS)
obstacle_nodePoint(id=9324, level=np.float64(-1.1825031694575236e-16), x=0, y=0, geotype=2, order=nan)障害物ノードの level 値が
convert_array_to_geometry では,境界条件(流線関数の境界値)を事前に指定することはできません.もし入力データが数値計算などで得たもので,具体的な境界データが事前に分かる場合には,追加された境界ノードの level 値を適切に設定するべきです.この値が理想的な境界条件からかけ離れている場合,この境界近傍の流れを表現する適切な COT 表現が計算できない場合がありますので,注意してください.もちろん,データの解像度が十分であれば,実用上は微小な誤差を無視しても構いません.
obstacle_node.level = 0.0 # 厳密な境界データが分かるので設定し直しておく(任意)これで,一通り入力空間データ geom の準備が整いました.Psi2tree で COT 表現を計算してみましょう.
psi2tree = Psi2tree(geom, threshold=0.0)
psi2tree.compute()計算が終わったら,結果を get_tree メソッドで取得します.get_tree で取得できる木構造データを,さらに convert メソッドを用いて,人が読みやすい形式に変換します.
from psiclone.cot import to_str
psi2tree.get_tree().convert(to_str)'a0(a2(L+,L-))'記号 a2 が,中央の障害物にぶつかる流れを表しています.無事,中央に障害物が一つ存在する一様流れのデータを表現できたことが分かります.
psiclone.util.mcdomain を用いて有界流れを解析する場合
次は psiclone.util.mcdomain.mcdomain_to_geometry() 関数を用いて多重連結領域を構成する例を見ます.mcdomain は multily connected domain (多重連結領域)の頭文字をとっています.先ほどと同じ要領で,今度は円環領域を入力空間に用います.
y, x = numpy.mgrid[-3:3:101j, -3:3:101j]
z = x + y * 1j
flow_domain = numpy.logical_and(numpy.abs(z) >= 1.0, numpy.abs(z) < 3.0)
obstacle_domain = ~flow_domain
plt.imshow(flow_domain, cmap="gray", origin="lower")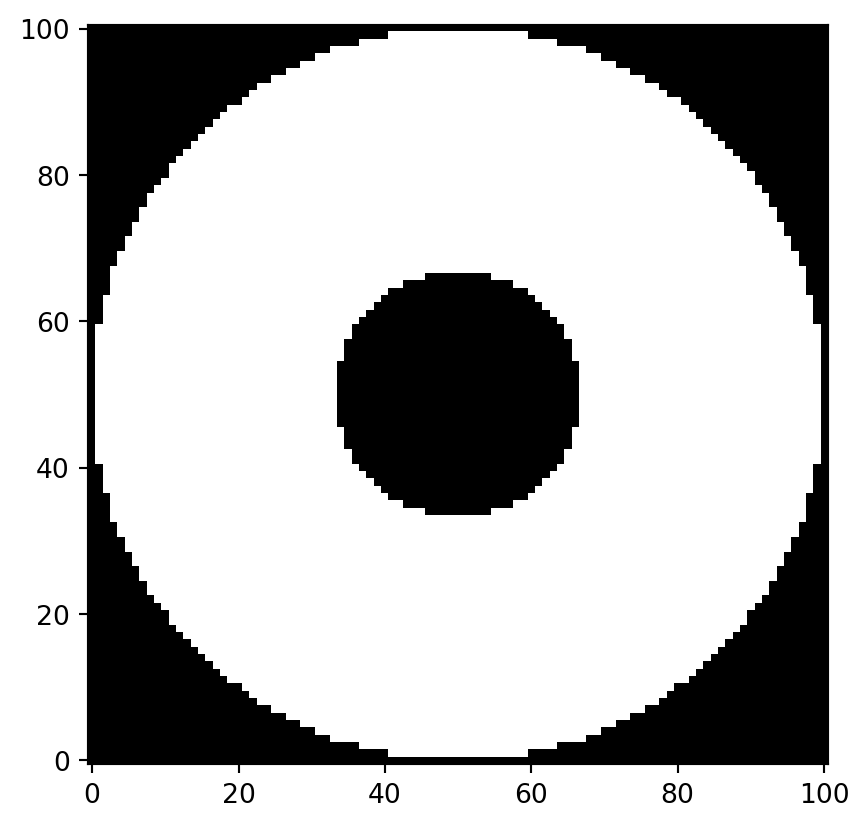
この円環領域の上で,テスト用のスカラー関数を定義します.ここでは,外側の境界条件として
z = x**2 + x + 1.5 * y**2
z *= x**2 + y**2 - 9 # 外側境界条件 z = 0 を強制
data = numpy.ma.masked_array(z, obstacle_domain, fill_value=numpy.nan)
plt.imshow(data, cmap="coolwarm", origin="lower")
plt.contour(data, colors="k")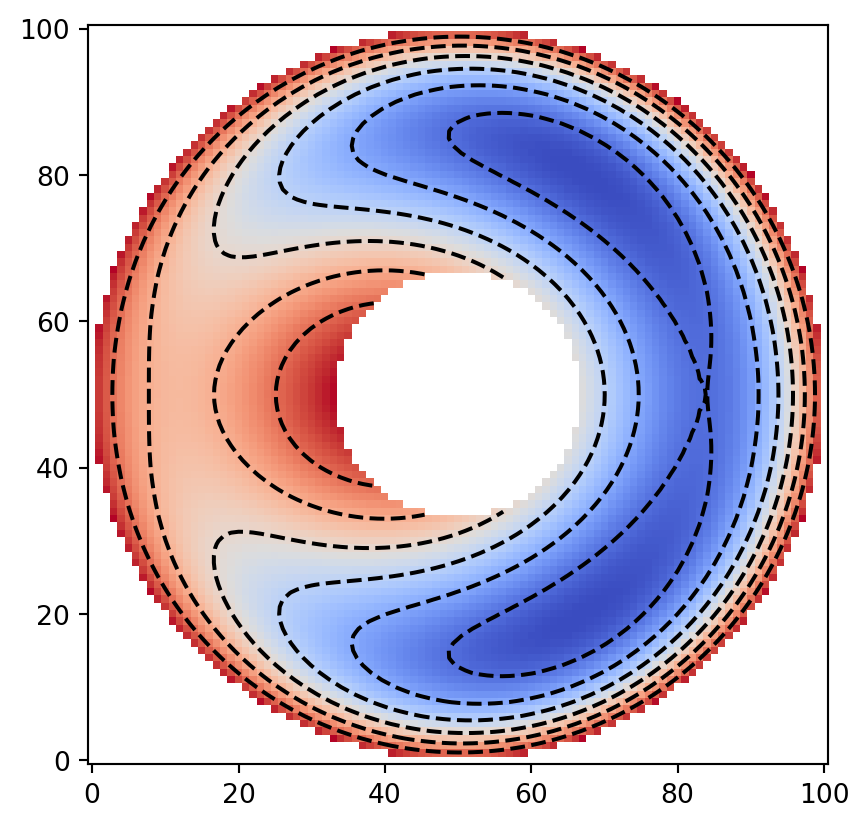
外側境界値がゼロになるよう boundary_condition オプションで外側境界条件を指定します.0 を直接するか,あるいは外側に向かってスカラー値が大きくなるデータなので,'max' を指定しても同じ効果が得られます.離散化によって,しばしば境界周りの流線トポロジーに意図しない微細なノイズが大量に発生します.'max' と 'min' はこの離散化の影響を効果的に抑制することができる便利なオプションです.一方で,内側境界周りの流線トポロジーのような特徴的な構造を捉えたい場合,'max' や 'min' よりも 'average' や 'mean' が便利です.状況に応じて適切な境界条件を指定することが重要です.
from psiclone.util.mcdomain import mcdomain_to_geometry
yi, xi = numpy.indices(data.shape)
geom = mcdomain_to_geometry(
xi.ravel(),
yi.ravel(),
data.ravel(),
boundary_condition=[
(Geotype.EXTERIOR, "max"), # 外側境界条件, 直接 0 を指定してもよい
(Geotype.OTHERS, "average"), # 内側境界条件
],
)/opt/build/repo/.venv/lib/python3.12/site-packages/psiclone/util/mcdomain.py:67: UserWarning: Warning: converting a masked element to nan.
nodes = OrderedDict(((i, j), UnionFind(isnan(z))) for i, j, z in zip(x_index, y_index, z))vis.draw_geometry(geom, bitmap=True)
plt.colorbar()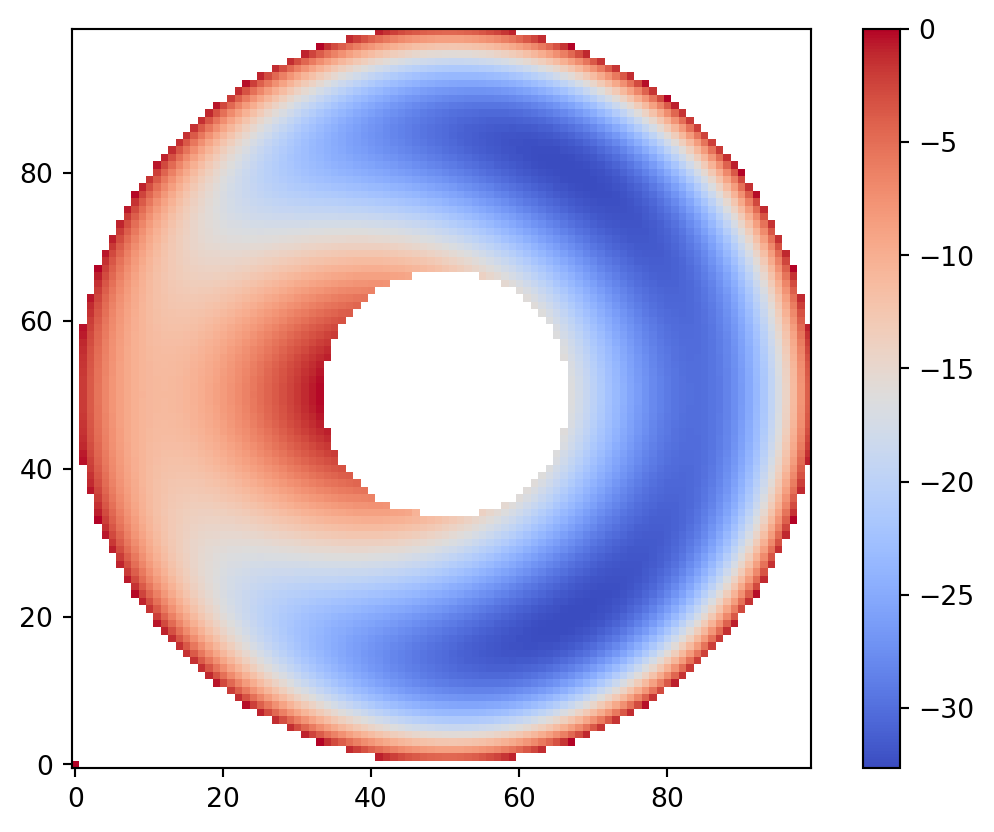
実際に計算してパーティション図と COT 表現を出力してみます.
from psiclone.cot import to_short_tex
psi2tree = Psi2tree(geom, threshold=1.0)
psi2tree.compute()
title = psi2tree.get_tree().convert(to_short_tex)
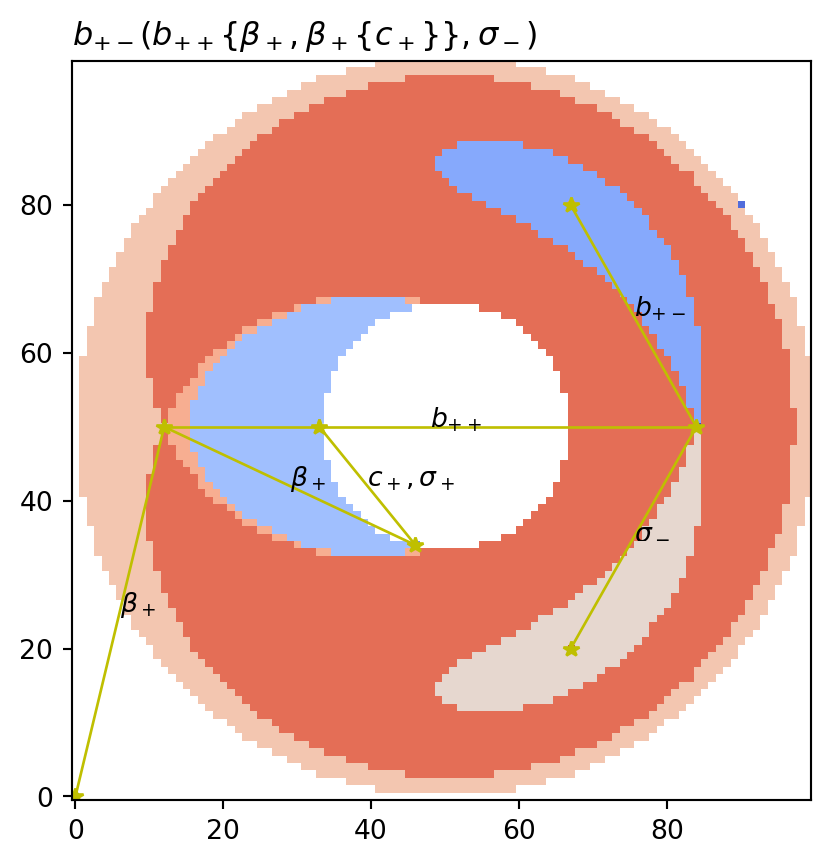
vis.draw_partition(psi2tree, bitmap=True, title=f"${title}$")
vis.draw_graph_markers(psi2tree)
vis.draw_COT_labels(psi2tree)