画像データに対する解析

データ読み込み

以下のようなグレースケール画像 toymodel.png を解析してみましょう。

画像を cv2 (OpenCV) を使って NumPy 配列として読み込みます．

import urllib.request

# 画像をダウンロードしてローカルファイルに保存する
with urllib.request.urlopen("https://psiclone.tfda.jp/asset/images/toymodel.png") as web_file:
    with open("toymodel.png", "wb") as local_file:
        local_file.write(web_file.read())

import cv2
import numpy as np

image_file_path = "./toymodel.png"
levels = np.array(cv2.imread(image_file_path, cv2.IMREAD_GRAYSCALE), dtype=np.float64)

levels を psiclone のデータ構造として読み込みます．

import psiclone.data

img = psiclone.data.GrayscaleImage(levels)

読み込んだ img を描画して，正しく読み込めているかを確認しましょう．

import matplotlib.pyplot as plt

import psiclone.visualization as vis

vis.draw_geometry(
    img,
    bitmap=True,
)
plt.colorbar()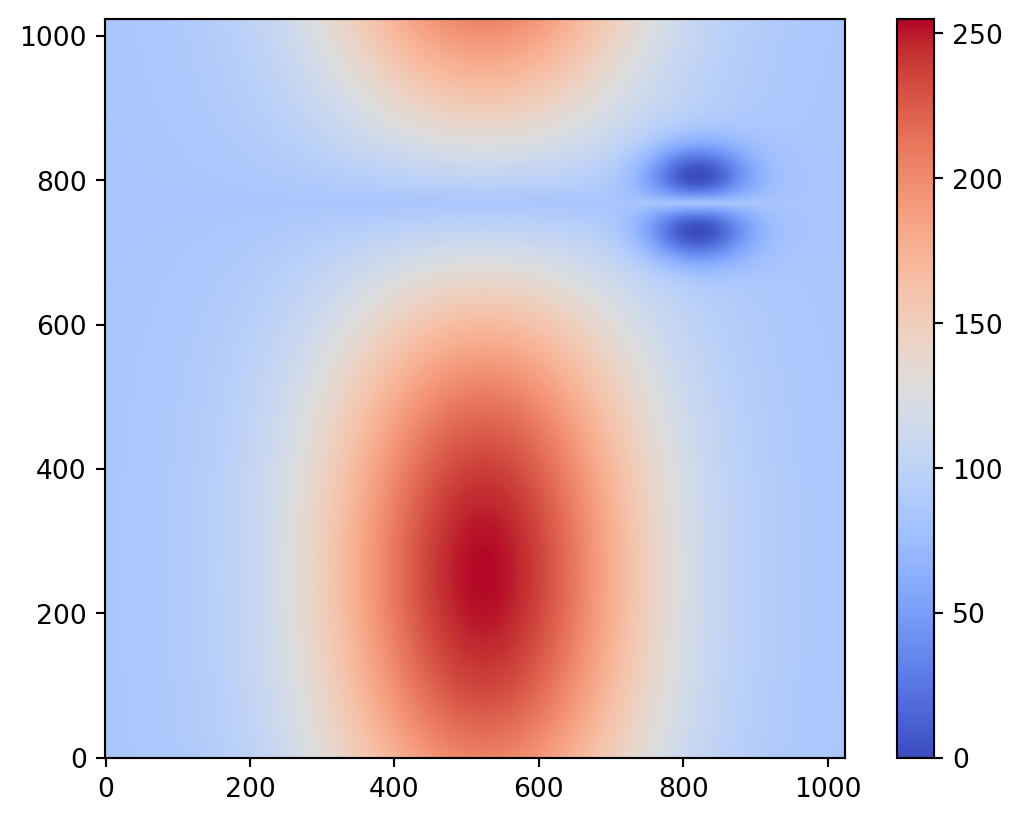

入力データのCOT表現への変換

読み込んだimgを解析して，partially Cyclically Ordered rooted Tree (COT) 表現を計算してみましょう．
これは，psiclone.psi2tree.Psi2tree クラスを使います．
入力データによってはここで非常に時間がかかるため，適切なノイズ除去閾値 threshold を設定する必要がある場合があります．
時間がかかりすぎる場合（他には結果の COT 表現が必要以上に細かい場合など）には，threshold をスケールに応じて1.0や10などに上げてください．

from psiclone.psi2tree import Psi2tree

psi2tree = Psi2tree(img, threshold=0)
psi2tree.compute()

COT表現への変換計算後, 計算結果を get_tree メソッドで取得します．
get_tree で取得できる木構造データを，さらに convert メソッドを用いて，人が読みやすい形式に変換します．

from psiclone.cot import to_str

psi2tree.get_tree().convert(to_str)

'a0(a-(b--{s-,s-}).a+(s+))'

convert メソッドに以下のいずれかを与えることで COT 表現を様々な出力形式へと変換できます．

psiclone.cot.to_str
- ギリシャ文字などを含まない簡易 ASCII フォーマットへ変換します
psiclone.cot.to_short_str
- psiclone.cot.to_str と同様ですが，情報を失わない範囲で冗長な記号を省略します
psiclone.cot.to_tex
- TeX 形式で正しい添字やギリシャ文字によるラベル付けをした形式へ変換します
psiclone.cot.to_short_tex
- psiclone.cot.to_tex と同様ですが，情報を失わない範囲で冗長な記号を省略します

convert に渡す関数を変えることで再帰的な変換をカスタマイズすることも可能です．

from IPython.display import Math, display

from psiclone.cot import to_short_str, to_short_tex

cot_tree = psi2tree.get_tree()
print(cot_tree.convert(to_short_str))
print(cot_tree.convert(to_short_tex))
display(Math(cot_tree.convert(to_short_tex)))

a0(a-(b--).a+)
a_\emptyset(a_-(b_{--})\cdot a_+)

$a_{\emptyset} (a_{-} (b_{- -}) \cdot a_{+})$

結果の可視化

入力データ (levels)・等高線図・レーブグラフ・COT 表現を重ねて描いてみましょう．

# 0. 画像解像度の設定
plt.rcParams["figure.figsize"] = [5, 5]
plt.rcParams["figure.dpi"] = 100

# 1. 画像上部に COT 表現を表示
plt.title(f"${psi2tree.get_tree().convert(to_short_tex)}$")

# 2. 入力データ (levels) と等高線図を描画
y = list(range(levels.shape[0]))
x = list(range(levels.shape[1]))
plt.imshow(levels, cmap="coolwarm", origin="lower", extent=[np.amin(x), np.amax(x), np.amin(y), np.amax(y)])
plt.contour(x, y, levels, colors="k")

# 3. レーブグラフと COT 表現を図に重ね描き
vis.draw_graph_markers(psi2tree, lw=2, edge_color="y-", node_color="g*")
vis.draw_COT_labels(psi2tree, fontsize=16)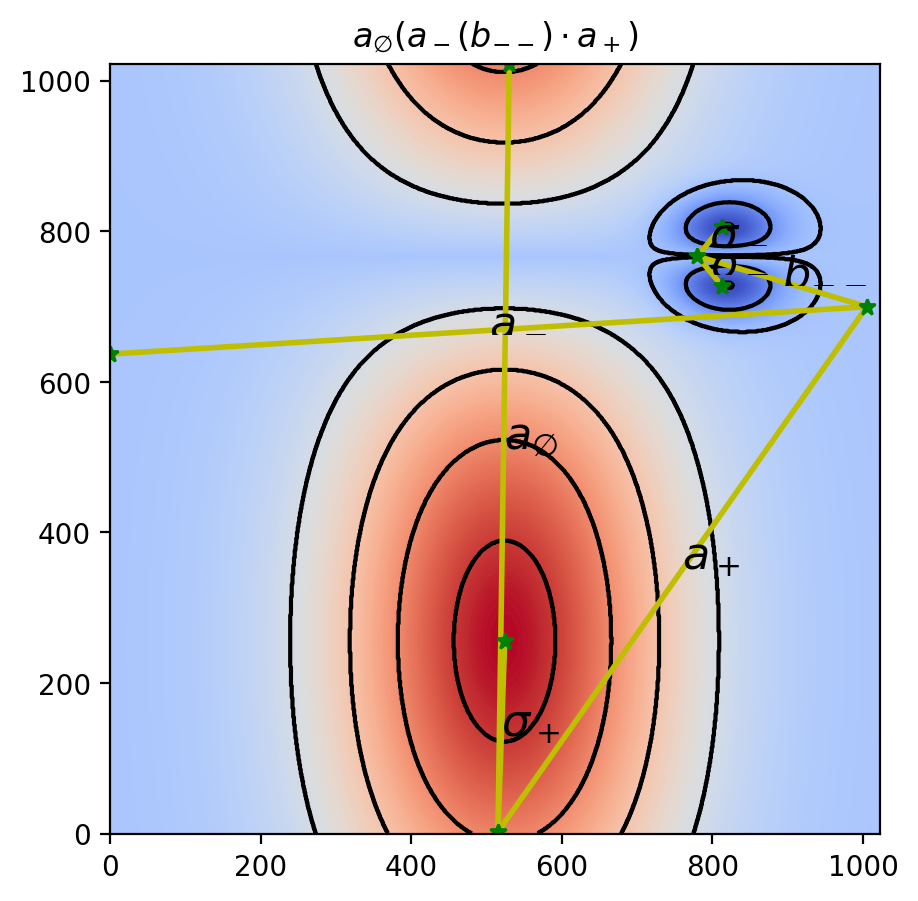

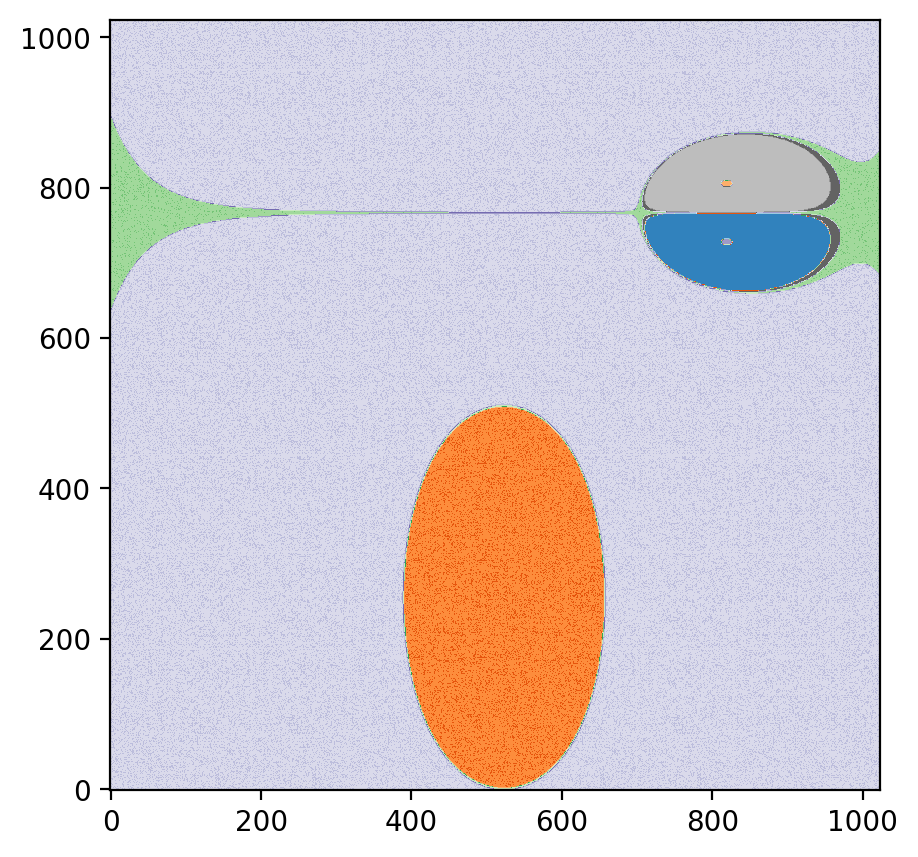
分割の可視化

数学的には，レーブグラフは同値関係による商空間として定まります．
psiclone で用いられているアルゴリズムでも，同値関係に基づく空間の分割が得られます．
分割を可視化するには，psiclone.visualization.draw_partition 関数が便利です．
これを見ると，レーブグラフを通して psiclone がどのように流線トポロジーを把握しているかがなんとなく分かります．

plt.rcParams["figure.figsize"] = [5, 5]
plt.rcParams["figure.dpi"] = 100
vis.draw_partition(psi2tree, bitmap=True, discrete=True, cmap="tab20c")